概要: 还垂直于平面 吗?设计意图:让学生明白要判定一条已知直线和一个平面是否垂直,取决于在这个平面内能否找出两条相交直线和已知直线垂直,至于这两条相交直线是否和已知直线有公共点,这是无关紧要的。根据试验,请你给出直线与平面垂直的判定方法。(学生叙写判定定理,给出文字、图形、符号这三种语言的相互转化)问题8:(1)与直线与平面垂直的定义相比,你觉得这个判定定理的优越性体现在哪里?(2)你觉得定义与判定定理的共同点是什么?设计意图:通过和直线与平面垂直定义的比较,让学生体会“无限转化为有限”的数学思想,通过寻找定义与判定定理的共同点,感悟和体会“空间问题转化为平面问题”、“线面垂直转化为线线垂直”的数学思想.思考:现在,你知道两位工人是根据什么原理安装旗杆的吗?为什么要求绳子在地面上两点和旗杆脚不在同一直线上?如果安装完了,请你去检验旗杆与地面是否垂直,你有什么好方法?设计意图:用学到手的知识解释实际生活中的问题,增强学生用数学的意识,同时通过提出 “
高一数学《直线与平面垂直的判定》教学设计,标签:教学设计,http://www.85jc.com
还垂直于平面
吗?
设计意图:让学生明白要判定一条已知直线和一个平面是否垂直,取决于在这个平面内能否找出两条相交直线和已知直线垂直,至于这两条相交直线是否和已知直线有公共点,这是无关紧要的。
根据试验,请你给出直线与平面垂直的判定方法。
(学生叙写判定定理,给出文字、图形、符号这三种语言的相互转化)
问题8:(1)与直线与平面垂直的定义相比,你觉得这个判定定理的优越性体现在哪里?
(2)你觉得定义与判定定理的共同点是什么?
设计意图:通过和直线与平面垂直定义的比较,让学生体会“无限转化为有限”的数学思想,通过寻找定义与判定定理的共同点,感悟和体会“空间问题转化为平面问题”、“线面垂直转化为线线垂直”的数学思想.
思考:现在,你知道两位工人是根据什么原理安装旗杆的吗?为什么要求绳子在地面上两点和旗杆脚不在同一直线上?
如果安装完了,请你去检验旗杆与地面是否垂直,你有什么好方法?
设计意图:用学到手的知识解释实际生活中的问题,增强学生用数学的意识,同时通过提出 “为什么要求绳子在地面上两点和旗杆脚不在同一直线上?”(对该问题可引导学生用三角形纸片来验证),从而来深化对直线与平面垂直判定定理的理解。
4.直线与平面垂直判定定理的应用
如图5,在长方体ABCD-A1B1C1D1中,请列举与平面ABCD垂直的直线。并说明这些直线有怎样的位置关系?

思考:如图6,已知
,则
吗?请说明理由。
(分别用直线与平面垂直的判定定理、直线与平面垂直的定义证明;并让学生用语言叙述:如果两条平行直线中的一条直线垂直于一个平面,那么另一条直线也垂直于这个平面)
设计意图:这个例题给出了判断直线和平面垂直的一个常用的命题,这个命题体现了平行关系与垂直关系之间的联系。
练习:如图,在三棱锥V-ABC中 ,VA=VC,AB=BC,K是AC的中点。
求证:AC⊥平面VKB
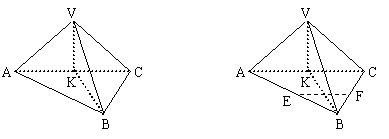
思考:
(1)在三棱锥V-ABC中,VA=VC,AB=BC,求证:VB⊥AC;
(2)在⑴中,若E、F分别是AB、BC 的中点,试判断EF与平面VKB的位置关系;
(3)在⑵的条件下,有人说“VB⊥AC, VB⊥EF, ∴VB⊥平面ABC”,对吗?
设计意图:例2重在对直线与平面垂直判定定理的应用.变式(1)在例2的基础上,应用了直线与平面垂直的意义;变式(2)是对例1判定方法的应用;变式(3)的判断在于进一步巩固直线与平面垂直的判定定理。3个小题环环相扣,汇集了本节课的学习内容,突出了知识间内在联系和融会贯通。
最新更新
推荐热门