概要: 【小编寄语】www.85jc.com数学网小编给大家整理了高一必修二《空间两直线的位置关系》练习题,希望能给大家带来帮助!重难点:理解异面直线的概念,能计算异面直线所成角;掌握公理4及等角定理.经典例题:如图,直线a,b是异面直线,A、B、C为直线a上三点,D、E、F是直线b上三点,A、BC、D、E分别为AD、DB、BE、EC、CF的中点.求证:(1) = (2)A、B、C、D、E 共面. 当堂练习:1.若a ,b是异面直线, b, c是异面直线, 则a ,c的位置关系是( )A.相交、平行或异面 B. 相交或平行 C.异面 D.平行或异面2.分别和两条异面直线都相交的两条直线的位置关系是( )A.异面 B. 相交 C.平行 D.异面或相交3.在正方体ABCD-A1B1C1D1中,与对角线AC1异面的棱有( )A.3条 B. 4条 C. 6条 D. 8条4.已知a ,b是异面直线,直线c平行于直线a,那么c与b()A. 一定是异面直线 B.一定是相交直线C. 不可能是平行直线 D.不可能是相交直线5.下面命
高一必修二《空间两直线的位置关系》练习题,标签:小学数学知识点,http://www.85jc.com
【小编寄语】www.85jc.com数学网小编给大家整理了高一必修二《空间两直线的位置关系》练习题,希望能给大家带来帮助!
重难点:理解异面直线的概念,能计算异面直线所成角;掌握公理4及等角定理.
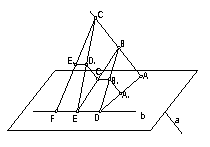
经典例题:如图,直线a,b是异面直线,A、B、C为直线a上三点,D、E、F是直线b上三点,A 、B C 、D、E分别为AD、DB、BE、EC、CF的中点.
求证:(1)
=
(2)A、B、C、D、E 共面.
当堂练习:
1.若a ,b是异面直线, b, c是异面直线, 则a ,c的位置关系是( )
A. 相交、平行或异面 B. 相交或平行 C. 异面 D. 平行或异面
2.分别和两条异面直线都相交的两条直线的位置关系是( )
A.异面 B. 相交 C.平行 D.异面或相交
3.在正方体ABCD-A1B1C1D1中,与对角线AC1异面的棱有( )
A.3条 B. 4条 C. 6条 D. 8条
4.已知a ,b是异面直线,直线c平行于直线a,那么c与b( )
A. 一定是异面直线 B.一定是相交直线
C. 不可能是平行直线 D.不可能是相交直线
5.下面命题中,正确结论有( )
如果一个角的两边与另一个角的两边分别平行,那么这两个角相等;
如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等;
如果一个角的两边和另一个角的两边分别垂直,那么这两个角相等或互补;
④ 如果两条直线同平行于第三条直线,那么这两条直线互相平行.
A. 1个 B. 2个 C. 3个 D.4个
6.下列命题中正确命题的个数是( )
两条直线和第三条直线等角,则这两条直线平行;
平行移动两条异面直线中的任何一条,它们所成的角不变;
过空间四边形ABCD的顶点A引CD的平行线段AE, 则
BAE是异面直线AB与CD所成的角;
④ 四边相等, 且四个角也相等的四边形是正方形.
A. 0 B. 1 C. 2 D. 3
7.已知异面直线a,b分别在
内,面
=c,则直线c( )
A.一定与a,b中的两条都相交 B.至少与a,b中的一条都相交
[1] [2] [3] [4] [5] [6] [7] [8] 下一页
最新更新