概要:的斜率k的取值范围.参考答案:经典例题:解: 直线AB的斜率k1=1/7>0, 所以它的倾斜角α是锐角;直线BC的斜率k2=-0.5<0, 所以它的倾斜角α是钝角;直线CA的斜率k3=1>0, 所以它的倾斜角α是锐角.当堂练习:1.A; 2.C; 3.C; 4.A; 5.B; 6.D; 7.D; 8.C; 9.C; 10.C; 11.C; 12.B; 13.D; 14. 00?a<1800; 15.- ; 16.300<α<600; 17.不存在;18.(1)由题意得 ,解得m=-2;(2)由题意得 ,解得 19. (1)依题意知三点共线,则有 , ,即2a-b=3为所求.(2) kAB= , kAC= ,∵A、B、C三点在一条直线上,∴kAB=kAC. 20.解: ,直线上一页 [1] [2] [3] [4] [5] [6] [7] 下一页
高一必修二《直线与方程》课堂练习,标签:小学数学知识点,http://www.85jc.com的斜率k的取值范围.
参考答案:
经典例题:
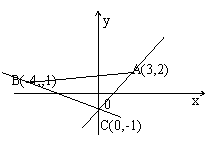
解: 直线AB的斜率k1=1/7>0, 所以它的倾斜角α是锐角;
直线BC的斜率k2=-0.5<0, 所以它的倾斜角α是钝角;
直线CA的斜率k3=1>0, 所以它的倾斜角α是锐角.
当堂练习:
1.A; 2.C; 3.C; 4.A; 5.B; 6.D; 7.D; 8.C; 9.C; 10.C; 11.C; 12.B; 13.D; 14. 00?a<1800; 15.-
; 16.300<α<600; 17.不存在;
18.(1)由题意得
,解得m=-2;(2)由题意得
,解得
19. (1)依题意知三点共线,则有
,
,即2a-b=3为所求.
(2) kAB=
, kAC=
,∵A、B、C三点在一条直线上,∴kAB=kAC.
20.解:
,直线
上一页 [1] [2] [3] [4] [5] [6] [7] 下一页
最新更新