概要:生独立思考,互相交流。生答:……学生回答不完整、不准确,同学之间可以给予提示,老师给予补充、指正。教师板书定义、图形。师强调:在平面内,由不在同一条直线的四条线段首尾顺次相接组成的图形叫做四边形。师质疑:在定义中,为什么要有“在平面内”这一条件呢?学生思考,教师出示自制的空间四边形模型。师:请同学们看老师这里的这个模型(空间四边形模型)。这个图形有几条边围成的?生答:4条。师追问:对!这4条边在同一平面内吗?生答:不在。师指出:这是一个空间四边形,即立体图形,立体几何我们将到高中系统学习。我们初中所说的四边形都是平面图形。所以,在四边形的定义中,“在平面内”这一条件必备。师质疑:同学们能给出五边形的定义吗?n边形(多边形)呢?师指出:如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形。如正三角形(等边三角形)、正四边形(正方形)、正五边形等等。点评 借助于自制的直观教具,说明四边形定义中“在平面内”这一不可省略的条件,
七年级下册《多边形的内角和》教学案例,标签:教学设计,http://www.85jc.com生独立思考,互相交流。
生答:……
学生回答不完整、不准确,同学之间可以给予提示,老师给予补充、指正。教师板书定义、图形。
师强调:在平面内,由不在同一条直线的四条线段首尾顺次相接组成的图形叫做四边形。
师质疑:在定义中,为什么要有“在平面内”这一条件呢?
学生思考,教师出示自制的空间四边形模型。
师:请同学们看老师这里的这个模型(空间四边形模型)。这个图形有几条边围成的?
生答:4条。
师追问:对!这4条边在同一平面内吗?
生答:不在。
师指出:这是一个空间四边形,即立体图形,立体几何我们将到高中系统学习。我们初中所说的四边形都是平面图形。所以,在四边形的定义中,“在平面内”这一条件必备。
师质疑:同学们能给出五边形的定义吗?n边形(多边形)呢?
师指出:如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形。如正三角形(等边三角形)、正四边形(正方形)、正五边形等等。
点评 借助于自制的直观教具,说明四边形定义中“在平面内”这一不可省略的条件,易于学生理解,化解了本课时的难点。
2、四边形及多边形的有关概念
师质疑:我们知道三角形有三条边、三个角。那么四边形、五边形的有关概念有哪些?
生答:也有边、角。
师在黑板上四边形的图形中标出边、角。
师指出:如图的四边形用表示它的各个顶点的字母来表示,可以按照顶点的顺序,记作“四边形ABCD".
点评 对于边、角这些能在图形中识别,而不要求学生掌握的描述性定义,采取学生类比
的边、角表示方法来归纳,渗透类比的数学思想方法。
师:对角线的概念学生从字面即可理解。如图,连接线段AC,线段AC是四边形ABCD的对角线。即在四边形中,连接不相邻两个顶点的线段叫做四边形的对角线。
师:如下表(多媒体展示),请同学们口答。
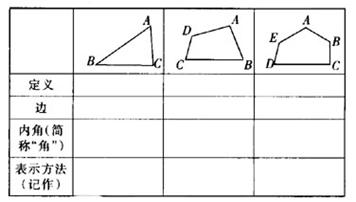
生口答上面表中的空格内容。
师:同学们回答的非常好!
师指出:如图1的四边形的任何一边向两方延长,如果其他各边都在延长所得直线的同一旁,这样的四边形叫做凸四边形。图2的四边形不是凸四边形。今后所说的四边形都是指凸四边形。

3、巩固性应用
师:请同学们口答下面的选择题。
(l)四边形的定义正确的是( )。
A、由四条线段首尾顺次相接组成的图形
B、在平面内,由四条线段首尾顺次相接组成的图形
C、平面内,四个点所确定的图形
D、在平面内,由不在同一条直线上的四条线段首尾顺次相接组成的图形
(2)下列命题中正确的是( )。
A、五边形中有两条对角线
B、如图3的四边形可以记作四边形ACBD
C、n边形有n条边、n个角
D、只有长方形和正方形是四边形

上一页 [1] [2] [3] [4] [5] [6] [7] [8] 下一页
最新更新