概要: 与x轴的交点M或与y轴交点N;或根据特殊情况的证法提示,过P点作x、y轴的平行线与直线 的交点R、S.或同时做x、y轴平行线.这样就收集到思路二、三、四.三种思路已经有了,它们的共性是什么?学生能观察出都在三角形中.我继续引导:能不能不构造三角形?而是其它数学相关量?我们刚学习了向量知识,能否用向量知识解决问题呢?(由于在前面学习的向量知识中,向量的模可以表示两点之间的距离,而证明两直线垂直时也已经用到向量知识,法向量又是本节课后阅读材料,本班学生基础和素质较好,在学习直线方向向量时已经布置阅读). 提出问题:线段的长度就是对应向量的模,那么如何求得向量 的模呢?根据实际情况提示一方面 的方向完全由直线的方向而定(与法向量共线),另一方面 的长度又与点P有关,它的长度又如何控制下来?所以有思路五,由师生一起分析,取法向量 = ,而 = ,以下只要求得上一页 [1] [2] [3] [4] [5] 下一页
高一必修二《点到直线的距离》说课稿,标签:数学说课,http://www.85jc.com
与x轴的交点M或与y轴交点N;或根据特殊情况的证法提示,过P点作x、y轴的平行线与直线
的交点R、S.或同时做x、y轴平行线.这样就收集到思路二、三、四.三种思路已经有了,它们的共性是什么?学生能观察出都在三角形中.我继续引导:能不能不构造三角形?而是其它数学相关量?我们刚学习了向量知识,能否用向量知识解决问题呢?(由于在前面学习的向量知识中,向量的模可以表示两点之间的距离,而证明两直线垂直时也已经用到向量知识,法向量又是本节课后阅读材料,本班学生基础和素质较好,在学习直线方向向量时已经布置阅读).
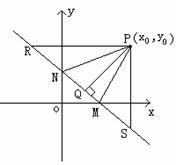
提出问题:线段的长度就是对应向量的模,那么如何求得向量
的模呢?根据实际情况提示一方面
的方向完全由直线的方向而定(与法向量共线),另一方面
的长度又与点P有关,它的长度又如何控制下来?所以有思路五,由师生一起分析,取法向量
=
,而
=
,以下只要求得
最新更新