概要:答:三角形BDC、AEB、AED与三角形ABC面积相等。7.下图中,大正方形是由9个面积相等的小正方形组成。以不在同一直线上的三个顶点组成三角形,这些三角形中有多少个与阴影三角形面积相等?想:找与阴影面积相等的三角形,实际就是找与它等底等高的三角形。为了方便,可分不同类型进行研究。解:把大正方形边长看作3,小正方形边长就是1,那么阴影三角形面积为3个面积单位。(1)边长是2,高是3的三角形个数:4×2×4=32(个)(2)边长是3,高是2,与(1)重复的不计入,个数是:8×2=16(个)合起来是:32+16=48(个)答:有48个三角形与阴影三角形面积相等。8.下图是一个棋盘,将一个白子和一个黑子放在棋盘线交叉点上,但不能在同一条棋盘线上,共有多少种不同的放法?想:黑子确定一个位置,白子就有6个不同的放法。而黑子总共有12个不同的位置,由此,便可推算出一共的放法。解:12×6=72(种)答:共有72种不同的放法。9.下图中有多少个长方形?多少个正方形?多少个三角形?想:由外向里,
游戏学数学 数图形,标签:数学游戏大全,http://www.85jc.com答:三角形BDC、AEB、AED与三角形ABC面积相等。
7.下图中,大正方形是由9个面积相等的小正方形组成。以不在同一直线上的三个顶点组成三角形,这些三角形中有多少个与阴影三角形面积相等?
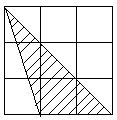
想:找与阴影面积相等的三角形,实际就是找与它等底等高的三角形。为了方便,可分不同类型进行研究。
解:把大正方形边长看作3,小正方形边长就是1,那么阴影三角形面积为3个面积单位。
(1)边长是2,高是3的三角形个数:
4×2×4=32(个)
(2)边长是3,高是2,与(1)重复的不计入,个数是:
8×2=16(个)
合起来是:32+16=48(个)
答:有48个三角形与阴影三角形面积相等。
8.下图是一个棋盘,将一个白子和一个黑子放在棋盘线交叉点上,但不能在同一条棋盘线上,共有多少种不同的放法?
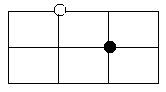
想:黑子确定一个位置,白子就有6个不同的放法。而黑子总共有12个不同的位置,由此,便可推算出一共的放法。
解:12×6=72(种)
答:共有72种不同的放法。
9.下图中有多少个长方形?多少个正方形?多少个三角形?

想:由外向里,从第二个和第四个正方形中数长方形个数。仍从第二和第四个正方形中数正方形个数,并加上四层的正方形。由内两层正方形和外两层正方形数三角形个数,再加上二、三两层正方形形成的三角形个数。
解:长方形个数:4+4=8(个)
正方形个数:4+4+4=12(个)
三角形个数:20+20+4=44(个)
答:有 8个长方形,12个正方形,44个三角形。
最新更新
推荐热门